Evaluation of derivatives using approximate generalized parameter shift rule

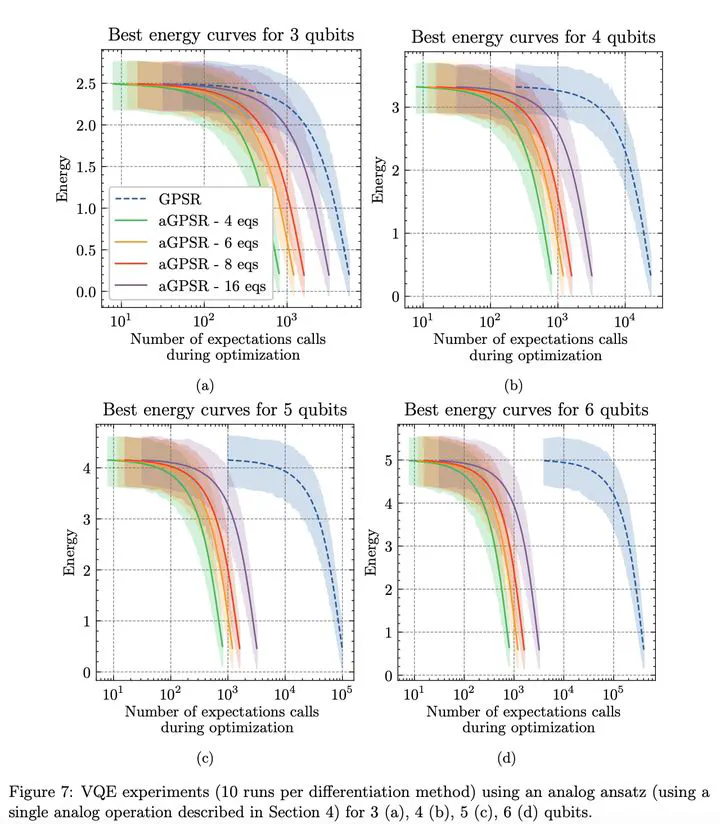
Parameter shift rules are instrumental for derivatives estimation in a wide range of quantum algorithms, especially in the context of Quantum Machine Learning. Application of single-gap parameter shift rule is often not possible in algorithms running on noisy intermediate-scale quantum (NISQ) hardware due to noise effects and interaction between device qubits. In such cases, generalized parameter shift rules must be applied yet are computationally expensive for larger systems. In this paper we present the approximate generalized parameter rule (aGPSR) that can handle arbitrary device Hamiltonians and provides an accurate derivative estimation while significantly reducing the computational requirements. When applying aGPSR for a variational quantum eigensolver test case ranging from 3 to 6 qubits, the number of expectation calls is reduced by a factor ranging from 7 to 504 while reaching the exact same target energy, demonstrating its huge computational savings capabilities.

Conference paper

Evaluation of derivatives using approximate generalized parameter shift rule”, Arxiv, 2025.